The sweetness of the scent of the rain would always be followed by long depressing blackouts — or power cuts as they say in India.
The heartfelt delight of school closures would always be followed by the blues from knowing that half of your town is under water.
The cheerful voice of the village grandfather would go numb due to one late-season havoc that takes out his bumper crop.
Monsoon was a difficult emotion growing up.
It has been an elusive puzzle for the thinkers and seekers. The history of its prediction is the history of its civilization. From the ancient sages who performed yajnas to appease Indra to the astrologers who captured the seasons in their calendar; From Vishnugupta’s insight of the importance of rainfall measurements to Varahamihira’s theory of clouds and their types, monsoon has always been the center of study.
That elusive monsoon has been a focus of study in our group too.
We have dedicated our energies to understanding and hedging water risk due to monsoon variations to complement other thorough monsoon prediction studies.
Arun Ravindranath, a Ph.D. candidate in the Department of Civil Engineering at the City College of New York, CUNY has pioneered a framework for quantifying and analyzing climate-induced water risk. He has been developing indicators for the assessment of climate-induced water risk, investigating the sources of predictability and developing statistically verifiable models for issuing season-ahead probabilistic forecasts for shortfalls.
His recent journal article published in Hydrology and Earth System Sciences (HESS) by Copernicus Publications is an important step in this direction and a valuable addition to the study of monsoon-induced risk in India.
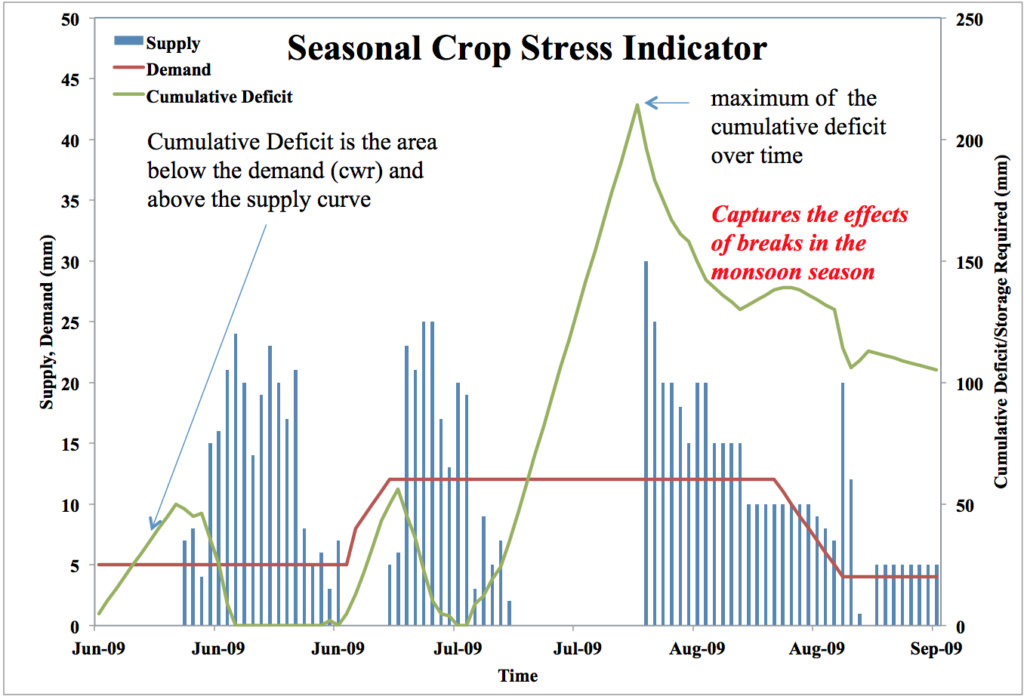
He developed a new crop water stress index called cumulative deficit index (CDI) to estimate water storage and irrigation requirements for agriculture in India.
He then concentrated on forecasting this crop water stress index a season-ahead as a means of providing advanced knowledge of water risk. Based on the hit and false alarm rates, the results achieved using our methodology were more favorable than precipitation forecasts issued by the India Meteorological Department.
Our method has a greater tendency toward strong and informative forecasts.
We are confident that this is a useful approach in investigating irrigation requirements and that our bootstrap-based uncertainty estimation is useful for developing probability-based management models for optimizing agricultural decisions.
You can get the paper from HESS website here. It is open access. If you need a copy of it, please write to Arun or me. We will be happy to share.
Arun Ravindranath has written it beautifully. Please read and let us know what you think.
“Sullen clouds are gathering fast over the black fringe of the forest. O child, do not go out!
… the rain-water is running in rills through the narrow lanes like a laughing boy who has run away from his mother to tease her.”
These were the words of the great Indian Poet, Rabindranath Tagore, when he expressed his love for Monsoon. It is but natural for the man who bears the same name to be smitten by Monsoon again.